Vincenty’s formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of the Earth, using an accurate ellipsoidal model of the Earth (e.g. the WGS 84 reference ellipsoid). The formulas were developed by Thaddeus Vincenty in 1975 and published in the Survey Review.
Direct Calculation
The first (direct) method computes the location of a point (CP) that is a given distance and azimuth (bearing) from another point (P1).
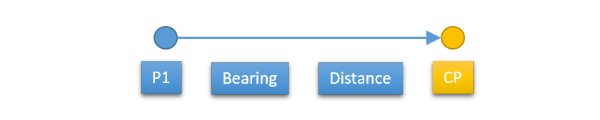
Inverse Calculation
The second (inverse) method computes the geographical distance and azimuth (bearings) between two given points (P1 and P2).

The calculations are based on the assumption that the figure of the Earth is an oblate ellipsoid and hence are more accurate than methods that assume a spherical Earth, such as great-circle distance.
Vincenty’s solution for the distance between points on an ellipsoidal earth model is widely used in geodesy because it is accurate to within 0.5 mm distance, 0.000015″ bearing, on the ellipsoid being used.
The simplest model for the shape of the entire Earth is a sphere. Since the Earth is flattened at the poles and bulges at the equator, the shape the Earth’s shape is not quite a sphere but rather an oblate (flattened) ellipsoid. The oblate spheroid, or oblate ellipsoid, is an ellipsoid of revolution obtained by rotating an ellipse about its shorter axis.
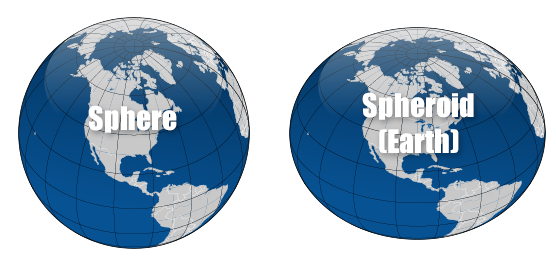
An ellipsoid of revolution can be uniquely defined by two numbers the semimajor axis and the flattening. The semimajor axis is represented by the radius at the equator. The shape of the ellipsoid is given by the flattening which indicates how much the ellipsoid departs from spherical. The current World Geodetic System (WGS-84) model uses a spheroid whose radius is 6.378,137 km at the equator and the reciprocal of the flattening is set at 298,257223563 exactly.
Leave a Reply